ベイズ統計について考えてみる

実はベイズ統計を単なる条件付き確率だと思っていた。確かに数式は同じだ。しかし、中身をよく見るとまるで違い、意味合いも異なる。

まず、条件付き確率とベイズの定理の数式を整理しておく。

■ 条件付き確率

■ ベイズの定理（ベイズ統計で用いられる数式）

ベイズの定理は、条件付き確率の式を変形したものであり、事前確率 P(A)P(A) を新しい情報 BB によって更新するための枠組みになっている。

条件付き確率の場合、母体の形状や平均、分散が既知であり、ある条件下で特定の事象が発生する確率を計算する。一方、ベイズ統計では条件が既知であるだけでなく、その情報を絶えず更新することで、特定の条件下における確率を推定していくことが可能になる。未知の状況でも、新たな情報が得られるたびに確率を動的に修正していくというのが特徴だ。

言い換えれば、情報がほとんどない状態でも、観測された情報を基に確率を推定していけるということだ。これは、静的な条件付き確率とは異なるダイナミックな性質をベイズ統計にもたらす。ベイズ統計を使うことで、状況の変化や追加のデータを反映しながら、より現実に即した推定を行うことができる。

この考え方に気づいたときは、かなり衝撃を受けた。というのも、情報が増えるにつれて、確率が大きく変化していくのだ。数学的な操作というより、現実世界での意思決定に直結したプロセスだと実感する場面は多い。

このことを教えてくれたのは、有名な投資家である清原達郎の『わが投資術市場は誰に微笑むか』だ。
わが投資術市場は誰に微笑むか

清原はベイズ統計を活用しながら、追加情報を逐次反映させて成長株への投資方法を洗練させてきた。証拠を積み上げることで、どのように投資リスクを最小化しつつリターンを最大化するかを示している点が興味深い。机上の理論にとどまらず、実際の投資行動に直結するところが彼のアプローチの強みだ。

この本に紹介されている例として、以下のものがある。

赤い車が20台、黒い車が80台ある状況を想定する。ある車が夜遅く、ほとんど光のない場所で事故を起こしたが、被害者は暗くて車の色をはっきり覚えていない。まずは単純に考えると、赤い車の割合が20%、黒い車の割合が80%なので、事故を起こした車が赤である確率は20%、黒である確率は80%という事前確率が立てられる。

しかし、その後の警察の聞き込みで、「事故を起こした車は赤色だった」という証言が得られた。仮にこの証言が100%正しければ、事故車両は赤と断定できるが、実際には暗闇での目撃情報なので完全な信頼は置けない。そこで、証言者の報告が正しい確率を70%、間違っている確率を30%と仮定してみる。

この状況を確率的に整理するには、条件付き確率だけでなく、ベイズの定理を用いた「事前確率のアップデート」が必要になる。考えられるケースは以下の2通りだ。

赤い車が事故を起こし、証言も正しい場合
黒い車が事故を起こし、証言が間違っている場合

まず1のケースの確率は、もともと赤い車である確率20%に証言が正しい確率70%を掛けた14%。
2のケースの確率は、黒い車である確率80%に証言が間違っている確率30%を掛けた24%。

すると、赤い車が事故を起こした確率は、

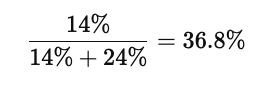
となる。これは事前の20%から16.8%上がった数値だ。比較的信頼できる証言が得られたことで、赤い車が事故を起こした可能性が高まったとみなせる。

次に、証言が正しくない場合を考える。証言が正しい確率を30%、間違っている確率を70%とする。

1のケースの確率は、20% × 30% = 6%
2のケースの確率は、80% × 70% = 56%

ここから、赤い車が事故を起こした確率を求めると、

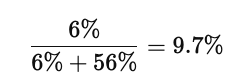
となり、証言の信頼度が低いと赤い車の確率も低く出ることがわかる。証言の精度が結果に多大な影響を与えることが、これでより明確になる。

さらに、最初の例に戻し、証言が正しい確率を70%にしたままで、もう一度「赤い車だった」という証言が出てきたとしよう。ベイズ統計では、この更新された事後確率を新たな事前確率として扱い、再度確率をアップデートできる。

すでに一度アップデートした後の赤い車の確率は36.8%、黒い車の確率は63.2%に変化している。もう一度同じ計算を適用すると、

赤い車（36.8%） × 証言が正しい確率（70%） = 25.76%
黒い車（63.2%） × 証言が間違っている確率（30%） = 18.96%

ここから2回目の証言後、赤い車が事故を起こした確率は、

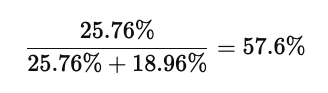
に上昇する。元の事前確率では赤い車の割合は20%だったが、比較的信頼度の高い証言が2回重なると、その確率は57.6%まで上がってしまうわけだ。

このように、証言が重なるほど、そしてその証言の信頼度が高いほど、赤い車が事故を起こしたと推定される確率がどんどん上乗せされていく。証言の正確性は、実際には何度も検証したり、別の情報源から裏付けを取るなどのプロセスで判断する必要があるが、いずれにしても、情報を逐次的に加味して確率を更新できるという点が、ベイズ統計最大の魅力だと言える。

この柔軟なアプローチによって、投資や医療、さらにはマーケティングリサーチなどのさまざまな分野で、ベイズ統計が活用されている。情報が追加されるたびに確率を更新し、より正確な推定へと近づけるという仕組みは、現実の意思決定において非常に役立つ。清原の投資戦略も、この考え方によって日々ブラッシュアップされているのだろう。

ベイズ統計は、条件付き確率の式そのものというよりは、未知の確率やパラメータを、集まった情報と合わせて動的に修正していく枠組みであり、実世界の不確実性に対処する強力な手段である。数式以上に、こうした更新プロセスに本質的な価値がある。