ベイズ統計学入門という本を借りてきた。非常に容易に書かれており、私には大変ありがたい本だ。
この本にある例題を解きながら自分の理解を深めていきたい。引用部分は太字で記入している。図表は、本にある内容を自分で作成してから転記している。小島先生の本は、素晴らしいので、直接本を読んでほしい。
例題
特定のがんに罹患していた場合、95%の確率で陽性となる検査を受けた結果、実際に陽性だったとする。このとき、自分ががんに罹患している確率は95%なのか?
答えは「NO」。
答えは、これだけでは分からないということだ。本をもう少し詳しく考えてみる。
がんの罹患率を0.1%(つまり、1,000人に1人ががんにかかっている)とする。
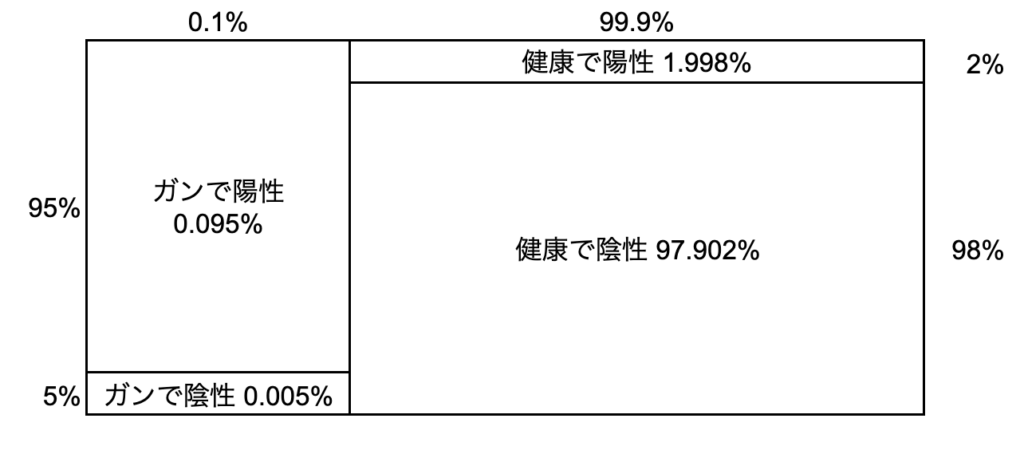
以下のような分類になるだろう。

また、この検査は、がんに罹患している人を95%の確率で正しく陽性と判定する。しかし、健康な人も2%の確率で誤って陽性と判定される。上記の情報を反映させると、以下のように分類される。

それぞれの確率を追加すると以下のようになるだろう。
この条件のもとで、検査結果が陽性だったとき、自分が本当にがんに罹患している確率を求める。
陽性であるということは、上記の分類から陰性の分類をなくせばいい。そのため、以下のような分類になる。
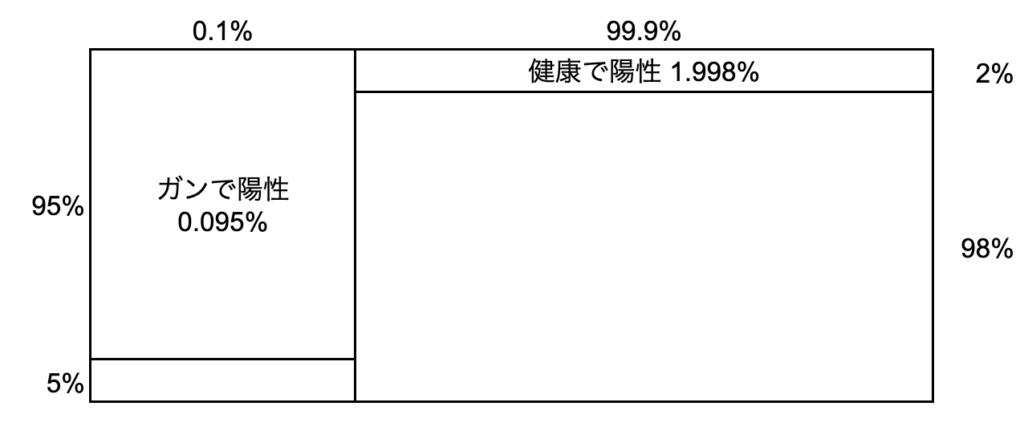
つまり、陽性と判定された割合は、全体で2.093%(=0.095%+1.998%) となる。その中で、ガンになっている確率を求めればいいから、0.095% / 2.093%=4.539% となる。
つまり、95%の確率でガンと判定されても、実際にはガンに罹る人が少なければ、かつ健康な人もそれなりの確率で陽性が出るのであれば、やっぱり陽性が出たとしても、ガンである確率は低いのである。
もう一度、おさらいをする。
がんに罹患している人と健康な人、それぞれが陽性と判定される確率を考える。
| 状態 | 陽性の確率 | 陰性の確率 |
|---|---|---|
| がんの罹患者 (0.1%) | 95% | 5% |
| 健康な人 (99.9%) | 2% | 98% |
ここで、がんの罹患率(事前確率)は0.1%なので、がんに罹患している人が検査で陽性と判定される確率は0.1%×95%=0.095%
一方、健康な人が検査で誤って陽性と判定される確率は99.9%×2%=1.998%
したがって、全体として陽性と判定される確率は0.095%+1.998%=2.093%
このとき、検査結果が陽性であった場合に本当にがんに罹患している確率(条件付き確率)は、以下のように求められる。0.095% / 2.093%=4.539%
つまり、検査で陽性と判定されたとしても、実際にがんに罹患している確率は約4.54%にすぎない。
がん患者の95%が陽性と出る検査であっても、他の条件等を調べないと実際にガンかどうかは判断できないケースが多いのだ。今回のケースでは、実際の罹患率と健康な人でも間違えて陽性と出る確率が必要なのである。もちろん、健康な人が100%陰性となるような検査であれば、陽性が出れば100%ガンに罹患していることになる。
どうだろう?。自分が知っている限りでは、最もわかりやすくベイズ統計を紹介している本だ。今後もこの本を読んでいき、小島先生から本経由で教えてもらった知識を私なりに消化していきたい。



コメント